In Model Extraction, Don’t Just Ask ‘How?’: Ask ‘Why?’
by Matthew Jagielski and Nicolas Papernot
In a previous blog post, we talked about model extraction attacks as a way for someone to steal a model that’s been made available to query. In the security jargon, we say that this attack targets the model’s confidentiality. The typical setup for a model extraction attack is the one of an API, such as the ones provided by MLaaS platforms, or a model served on an edge device, such as the image models found in many of our smartphones. In both cases, the adversary is able to send inputs to the model and observe the model’s prediction, but they do not have access to the model’s internals. The goal of model extraction is to recover these details.
This may seem like a simple enough threat model, but there are a lot of subtleties and variants, which we argue impact the strategy an adversary should follow. This is one of the main arguments in our paper “High Accuracy and High Fidelity Extraction of Neural Networks” to appear this summer at USENIX Security 2020. The crux of our paper is that designing an effective extraction attack requires that one first settle on a few critical details—the adversary’s goal, capabilities, and knowledge.
Accuracy or Fidelity? Which one should I care about?
In general, adversaries may be interested in stealing a model for two reasons. They could be purely motivated by the act of theft: one example is if they plan to later reuse the stolen copy of the model for their own financial benefit. Alternatively, stealing the model could be a stepping stone towards another attack. In other words, the adversary is motivated by reconnaissance.
A theft-motivated adversary simply wants to stop paying for the API, and wants to reconstruct its general behavior. A reconnaissance-motivated adversary, however, is more focused on the specifics of the given model, perhaps to later more easily compromise the security or privacy of the model. We propose that a theft-motivated adversary is interested in high accuracy extraction, while a reconnaissance-motivated adversary is more interested in a high fidelity extraction reconstruction. We call the limit of high fidelity, where the stolen model exactly matches the victim model, functionally equivalent extraction.
How does this look in practice? Let’s take a simple linear model and illustrate the different extraction goals.
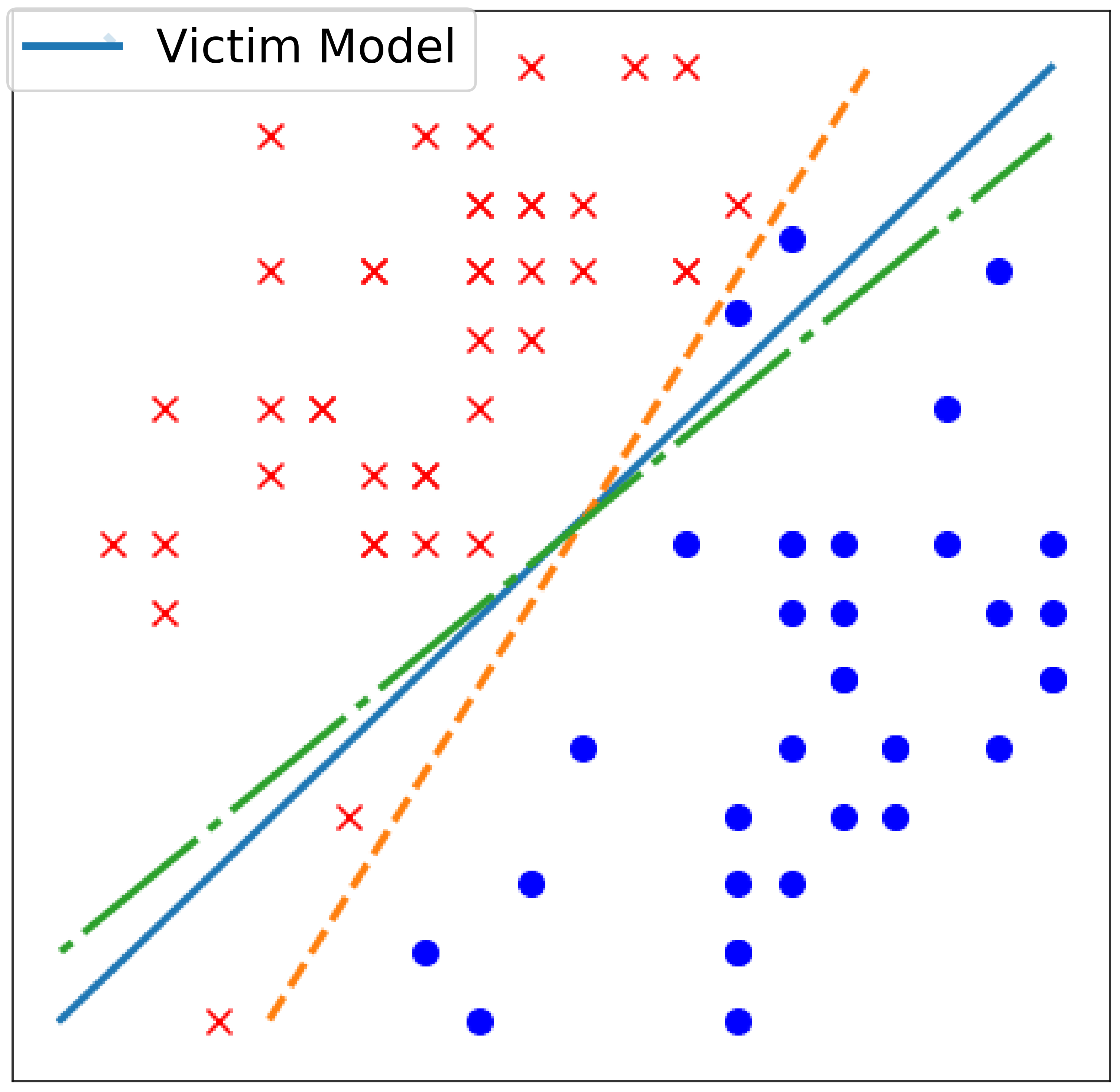
In this figure, the blue line is the true decision boundary. A functionally equivalent extraction attack would recover it exactly. Recovering the green line is still high fidelity. Why? Because the green and blue models make exactly the same predictions on all inputs here: when a point is on one side of the blue line, it is on the same side of the green line as well. But recovering the orange line compromises fidelity for a gain in accuracy. You can see that by looking at the two red crosses and two blue dots, which the blue and green lines incorrectly classified but which the orange line correctly classifies. A theft-motivated adversary would prefer the orange line to the green, but a reconnaissance-motivated adversary would prefer the green to the orange.
Why does this matter? Beyond the academic aspect of the question (having a precise taxonomy for model extraction makes it easier to compare different works, identify open problems, and allows for rigorously evaluation of defenses), we argue that our taxonomy identifies two interesting phenomena about model extraction:
Most of the approaches previously proposed have focused on high accuracy. The canonical approach to model extraction has the victim model label a bunch of unlabeled points which the adversary used to train their own copy of the model. In our paper, we start by improving over these learning-based attacks to make them more query efficient. Achieving high fidelity extraction, and in the limit functionally equivalent extraction, is going to require a completely different approach. That’s because the retraining attack only requires that the stolen model match the correctness of the prediction, not the fact that the stolen model makes these predictions in the same way as the victim model. For this reason, we also explore a new form of attack in our paper, and demonstrate that it can perform functionally equivalent extraction of real 2-layer ReLU networks.
How far can we take learning-based approaches?
The most natural approach to model extraction is a learning-based attack. The simple observation this approach uses is that the defender got the model by running a learning algorithm in the first place, so we should also be able to steal a reasonable model by learning. The adversary still gains something because they don’t have to label a training set, which is usually an expensive step of the ML process. Instead, the adversary exploits the victim model to obtain labels: the adversary sends inputs they would like to train on to the victim and the victim responds with the inputs’ labels.
Because the adversary obtains labels for their training data by querying the victim model, the adversary would like to be able to train their stolen copy with as few labels as possible. Each label means one query to the victim, and this may increase the cost of the attack (for instance, if the victim model charges for each query answered) or it may make it more likely that the adversary is detected as abusing the victim model by submitting too many queries. Thus, a model extraction attack that is learning-based should be as query-efficient as possible.
This means that the most effective techniques for this should also be the most query-efficient techniques for machine learning. For example, active learning has been shown to be amenable to model extraction attacks (see Tramer et al. or Chandrasekaran et al.). Active learning is a form of machine learning where rather than having a completely labeled training set to start with, one starts with an initially unlabeled dataset and decides what labels to obtain based on the value that the label is believed to provide to learning. A common strategy is to ask for labels on inputs for which the learning algorithm is currently very uncertain.
Another form of machine learning, semi-supervised machine learning, is similar to active learning but uses the unlabeled data in addition to the labeled data to learn. We consider an adversary with a large set of unlabeled data, which a theft-motivated adversary is likely to have (indeed, they have a lot of data, and are trying to alleviate the cost of querying on all of this data!). In our paper, we show that semi-supervised learning can be effective in this setting, and the adversary only needs to query on a small fraction of their dataset. This leads to very effective high accuracy extraction attacks.
How far can we take this idea? Can we achieve functionally equivalent extraction with a learning-based approach? To tease things apart, we asked ourselves how would an adversary perform if it had perfect knowledge of the training process used to train the victim model? That is, would an adversary aware of the optimizer, the model architecture, and the exact training data used by the defender be able to replicate exactly the same model through a learning-based approach? To answer this question, we considered the following experiment: we ran the defender’s learning algorithm twice. If the learning process is completely deterministic, then we’ll get two identical models. However, that turns out not to be the case. We observe that initialization randomness, batch randomness in SGD, and even GPU nondeterminism prevent functionally equivalent extraction for neural networks. This is illustrated in Table 4 of our paper. This means that even if the adversary knew everything about the defender’s setup, which is clearly unrealistic, they would not be able to achieve a high-fidelity extraction through a learning-based approach.
Next, we asked: if this nondeterminism is a fundamental limit of existing learning-based approaches, what can we do if we want to achieve functional equivalence?
Directly recovering weights of 2-layer networks for functionally-equivalent extraction
In principle, functional equivalent extraction of a neural network is a tough thing to do. That’s because a neural network can represent very complex decision surfaces. Consider even a very simple case: a 2-layer ReLU network (two weight matrices, separated by ReLU activations), with no softmax layer. Extraction even in this setting is troubling; each ReLU can be in one of two states: active or inactive, so the neural network is a piecewise linear function with what could be exponentially many regions. Here’s an illustration of what such a neural network’s output surface could look like:
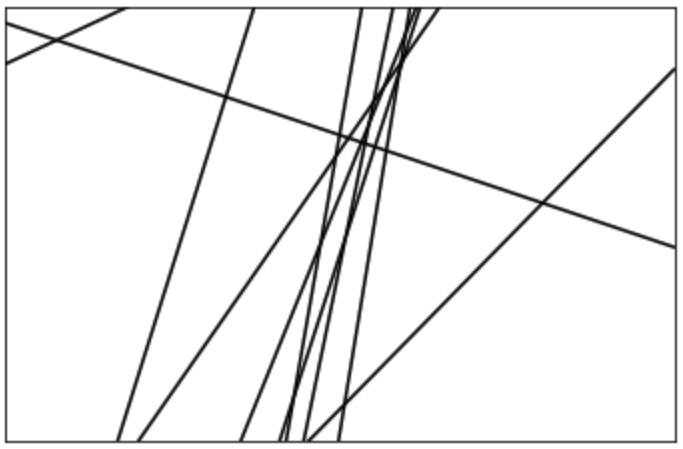
For this case, though, Milli et al. came up with an efficient extraction algorithm. It works by leveraging one simple idea: as we move along a line in input space, the network is piecewise linear. That’s it. We need to find those places (which we call critical points), where the linearity breaks. These inputs are at one ReLU’s boundary: moving in one direction, it’s inactive, while moving in the opposite direction, it’s active. By probing the network to identify what the linear function is on either side of the boundary, we can see how the network’s output differs when the network is active from when it’s inactive. This difference can be used to exactly reconstruct the weights that contribute to that ReLU’s input. Once we find the weights for every ReLU, we can piece them together to make the full model. This involves a couple technicalities, like distinguishing between a ReLU being active and inactive, and reconstructing the last layer, which is generally not made up of ReLUs.
However, the Milli et al. paper only shows how to do this when the network is computed exactly, with real number arithmetic. In particular, it fails when using floating-point arithmetic. In our paper, we made a couple improvements to the algorithm. First, we made finding critical points more query efficient, with an improved search procedure. We also showed a simpler way to figure out if a ReLU is active or inactive. Most importantly, we made it work in practice, with float64 arithmetic. The main way to do this was by improving the error tolerance; we sometimes incorrectly measure a weight, but we showed how to recover from these errors using a learning-inspired approach. In a follow-up work, we show how to extend this technique to deeper neural networks!
Conclusion
Model extraction is far from being a simple vulnerability. Our work shows that we still understand relatively little of the attack surface. In particular, while our high-accuracy attacks scale up to very large models, we find that high-fidelity attacks have a lot of potential for adversaries interested in specificities of the victim model’s decision surface. The latter could serve as the basis for realistic attacks on the privacy of training data. We believe that there is a lot of work to be done to explore these two model extraction attack goals, and also hybrid strategies that combine the advantages of different high-accuracy and high-fidelity approaches. We report preliminary investigations in our paper.
Defending against model extraction remains an open problem. Our taxonomy asserts that defending from model extraction requires identifying the type of model extraction we would like to prevent. We prove in our paper that functionally-equivalent extraction is hard to achieve for worst-case neural networks, and discuss recent work suggesting that limited access assumptions can prevent fidelity extraction for some models. However, with stronger access assumptions, or for different models, fidelity extraction and accuracy extraction may be impossible to defend against, given enough queries and if the victim provides accurate outputs. In the event that a goal is impossible to defend against, the community has started experimenting with watermarking as an attempt to claim ownership of stolen models, in a process that is the analog of DRMs for music and movies.
Acknowledgments
The paper this blog post is based on was written jointly with Nicholas Carlini, David Berthelot, and Alex Kurakin. The follow-up work on direct recovery was done by Nicholas Carlini, Matthew Jagielski, and Ilya Mironov. We also thank Nicholas Carlini and Varun Chandrasekharan for helpful feedback on drafts of this blog post.