Are adversarial examples against proof-of-learning adversarial?
by Congyu Fang, Hengrui Jia, Varun Chandrasekaran, and Nicolas Papernot
Machine learning models are notoriously difficult to train, and obtaining data to train them is also a challenging proposition. These trained models are often used in many safety-critical situations, and their provenance is of utmost importance. However, recent news suggests that models deployed in such settings are susceptible to being stolen. What does one do in such settings?
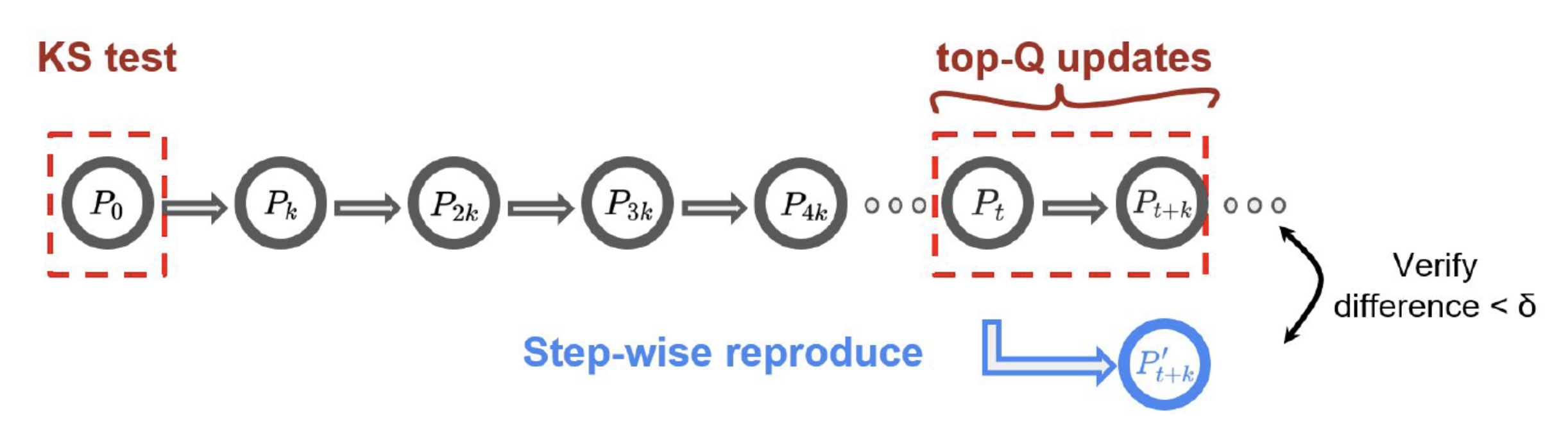
Jia et al. propose a non-cryptographic protocol, “Proof-of-Learning (PoL)”, that can be used to “prove” the computation expended towards training a deep learning model. PoL works as follows: during the time of training (or proof creation), the model owner (prover) keeps a log that records all the information required to reproduce the training process at regular intervals. This log comprises of states which include (a) the weights at that particular stage of training, (b) information about the optimizer, (c) the hyperparameters, (d) the data points used thus far, and (e) any other auxiliary information (such as sources of randomness) required to reach the next state (i.e., weight/checkpoint) from the current state. At the verification stage, the verifier (a trusted third party) would take a state from the PoL, perform the computation required for training to see if it can reproduce the next state recorded in the PoL. In an ideal world with no noise or stochasticity, the reproduced model state should be identical to the state logged in the PoL.
However, due to the stochasticity arising from both hardware and software, perfect reproducibility cannot be achieved. Hence, to avoid a false rejection, the verifier would need to set an error threshold to tolerate this discrepancy.
Vulnerabilities of Proof-of-Learning
PoL suggests to verify the training process based on the hyperparameters provided by the prover, but the PoL verification protocol cannot verify the correctness of the hyperparamaters. This means that if the adversary has gained white-box access to a model, the adversary can “manipulate” the verification process by providing arbitrary training hyperparameters, and spoof the PoL protocol (that is, trick the verifier into validating the claim of ownership for the stolen model). Here are some examples of how this can be done:
-
Error Tolerance: In the status quo, the verifier will need to carefully select a fixed value for the reproducing error tolerance based on the hyperparameters reported by the prover. The error tolerance should be chosen such that it is greater than the largest error induced by stochasticity throughout the entire proof creation process. This could be exploited by an adversary to generate a falsified proof.
-
Selection Heuristics: In addition, the verifier only verifies a subset of states in the proof to improve the verification efficiency. An adversary could construct a proof by exploiting the selection heuristics, and cause the verifier to only verify those steps it creates (in order to pass verification).
-
Public Data: Finally, in the status quo, the PoL proposes two variants to include information about the training data used in the PoL. The first requires public data release. The second instead requires that the PoL come with a hash of the data only. The former may cause unnecessary privacy leakage or violations, and can also be exploited by adversaries to create falsified proofs.
“Adversarial Examples” for Proof-of-Learning?

Recent work by Zhang et al. exploits the aforementioned shortcomings (particularly related to error tolerance and public data release) to create “invalid” proofs that pass verification. Here, an invalid proof refers to a proof that involves the states that are not from a legitimate/honest training process. Also, the computational cost to create such an invalid proof should ideally be much less than that of honest training. They utilise the following two techniques.
Synthetic Adversarial Updates (exploiting public data access): It is conceivable that, given access to the training data, an adversary can modify it slightly such that training on the modified data results in a jump from an initial state to any arbitrary state (including the final state). Such an attack was proposed, but not evaluated: the authors found that the optimization problem involved to modify data that achieves such a one-step jump was difficult & unstable. There is also no theory to understand when such a strategy would work and when it wouldn’t.
The problem is exacerbated when the adversary is denied access to the data used for training. This could be done in PoL by releasing hashes of the training data along with the proof, rather than the data itself. Here, the aforementioned optimization problem is to be designed to “synthesize” data to meet such a one-step jump. This too, was observed to be difficult, unstable, and devoid of any theoretical intuition.
Synthetic Checkpoint Initialization (exploiting static choice of error tolerance): Recall that the verifier sets an error tolerance to account for hardware and software stochasticity. At the time of verification, if the reproduced state is within this threshold, then the step passes verification (as witnessed in the figure). A simple strategy an adversary could exploit is to create synthetic states which lie within this threshold. The adversary does so by linearly interpolating between the initial and final state, such that the distance b/w any two pairs of states is significantly lesser than the error tolerance. Then, the adversary can modify the data (using techniques described earlier) such that the state transitions (b/w these “close” states) are possible.
However, optimizing for the data points that lead to such state transitions is a second order non-convex problem in the setting of deep learning, which is computationally costly, and can potentially exceed the cost of training. Also, similar to the previous attack, there’s no guarantee that this would converge, especially when data access is restricted.
Despite these impressive results, there is one item of major discrepancy. Let’s look at this figure (Figure 1 from the PoL paper):
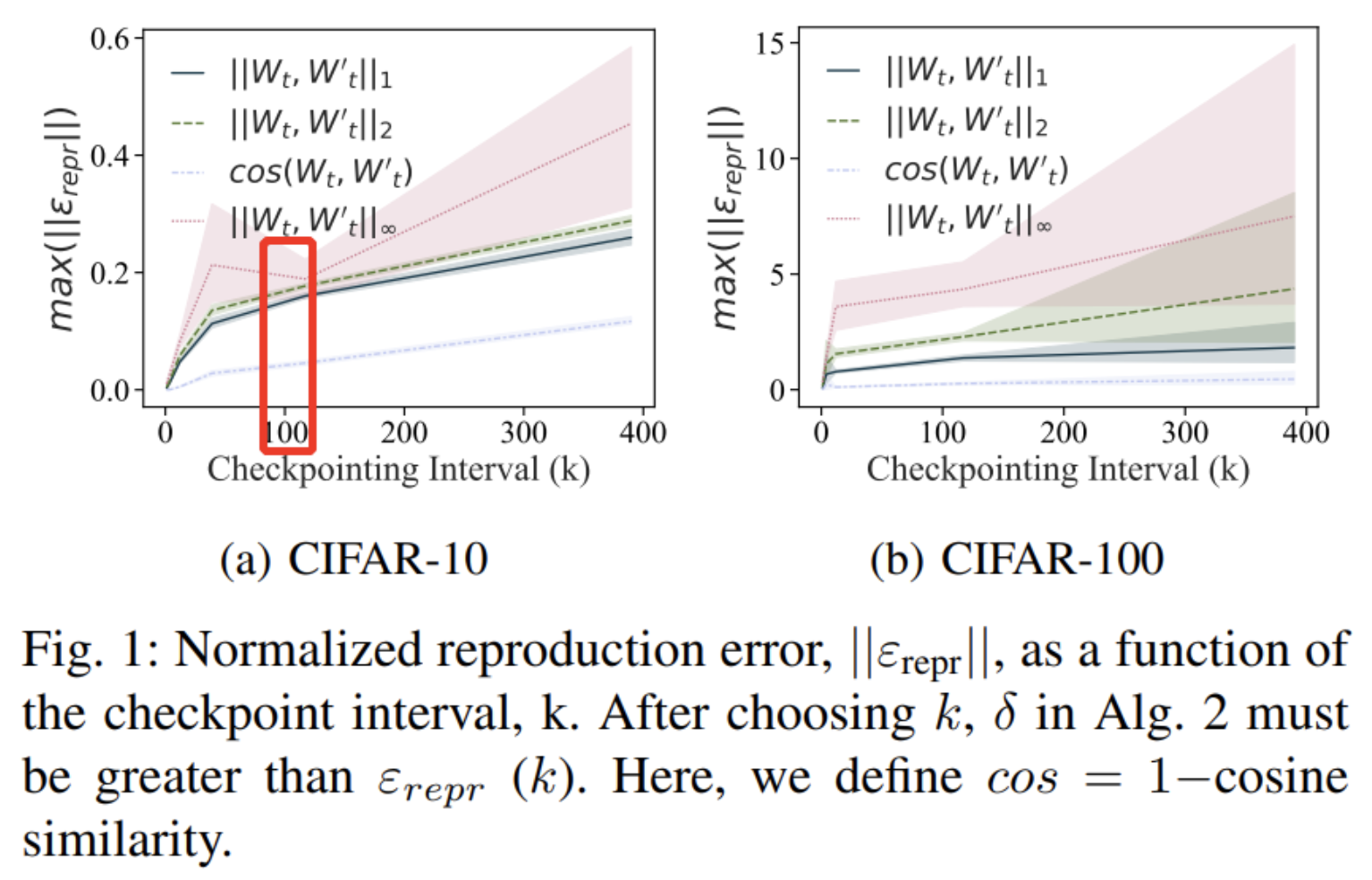
This figure plots the reproduction error as a function of checkpoint interval (i.e., how frequently states are logged in the PoL). It suggests that the reproduction error cannot be eliminated and may be large when we do not checkpoint frequently enough, due to inherent randomness in training DNNs. A checkpoint interval of 100 is circled in red because this was used in attacks against PoL.
In the attack paper, we instead see that the vertical axis on the following figure is smaller by an order of 10:
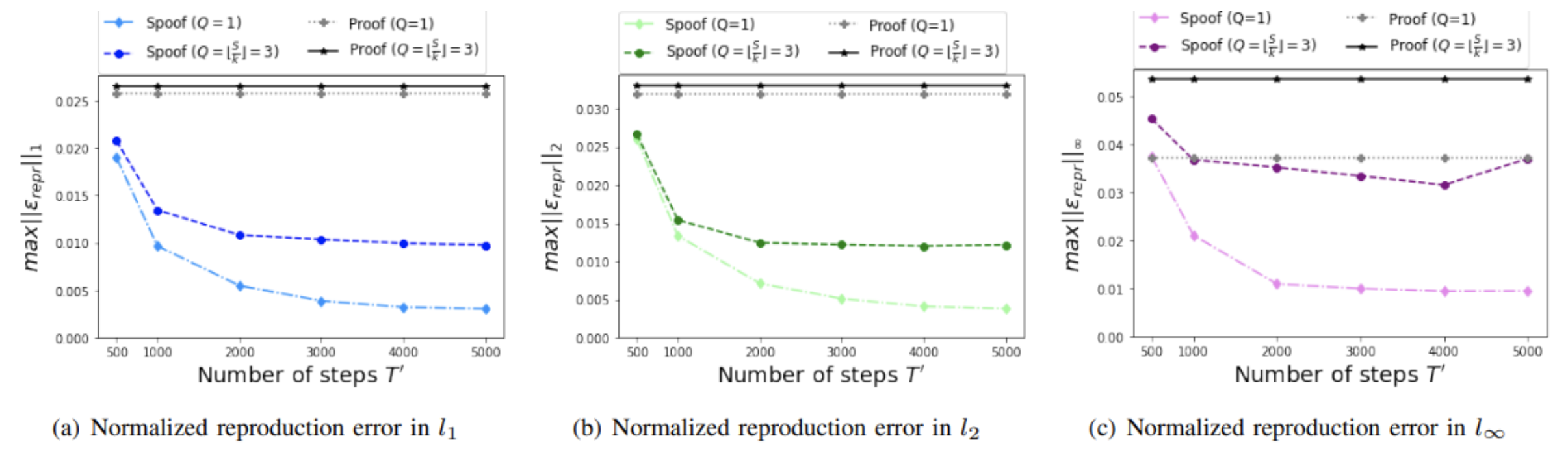
How could the reproduction error (even for the benign proofs) be smaller by an order of 10 in the attack paper? In the PoL paper, when experiments for the PoL creation and PoL verification were conducted on two different machines, trying the best to fix all source of randomness including using deterministic operations provided by PyTorch was unable to reduce the error by this much; and only conducting the experiments on the same machine could lead to such a small error. This suggests that the authors of the attack paper tested their attack and verified it on the same machine. In other words, this would amount to implicitly assuming that the adversary is capable of using the same machine than the verifier uses. This is a strong assumption, at which point the attacker has gained capabilities that make attacking PoL futile. Unfortunately, at the time of writing, the authors did not provide us with code to reproduce their results.
Additionally, the attack paper assumes that the adversary has the ability to control the checkpointing interval. This is a misunderstanding of the original PoL paper, where the verifier should be the one setting this parameter. In fact, by simply using a smaller checkpointing interval (i.e. k=10), it is found that the proposed attack failed for the CIFAR-100 dataset.
Conclusions
In conclusion, the original proposal does have some vulnerabilities which open a previously unseen attack surface. However, as we have explained earlier, these issues are easily addressed once the adversary is prevented from directly accessing the training data. The original PoL paper describes a mechanism to do just that: provide a hash of the data along with the PoL, rather than the data itself. Our discussion suggests that in such settings, the optimization problem required to create falsified proofs does not converge (and there’s currently no theoretical intuition as to when it may). Coupled with timestamping of the PoL (as discussed in the original PoL proposal), this greatly reduces the aforementioned threat surface.