Can stochastic pre-processing defenses protect your models?
by Yue Gao, Ilia Shumailov, Kassem Fawaz, and Nicolas Papernot.
Defending against adversarial examples remains an open problem. A common belief is that randomness at inference increases the cost of finding adversarial inputs. For instance, one could apply a random transformation to inputs prior to feeding them to the model. Evaluating such defenses is not easy though. This is because of the complicated transformation and high computational costs.
In this blog post, we outline key limitations of stochastic pre-processing defenses and explain why they are not supposed to make your models more robust to adversarial examples.
This is important because there is an increasing effort to improve defenses through a larger randomization space or more complicated transformations. For example, BaRT [1] employs 25 transformations, where the parameters of each transformation are further randomized. This makes it even more difficult to evaluate stochastic pre-processing defenses. In fact, due to the complexity of the BaRT defense, it was only broken recently (three years later) by Sitawarin et al. [2] with a complicated adversary-aware attack.
Put another way, it is unclear how future defenses can avoid the pitfalls of existing stochastic pre-processing defenses, largely because these pitfalls remain unknown.
Most stochastic defenses lack sufficient randomness
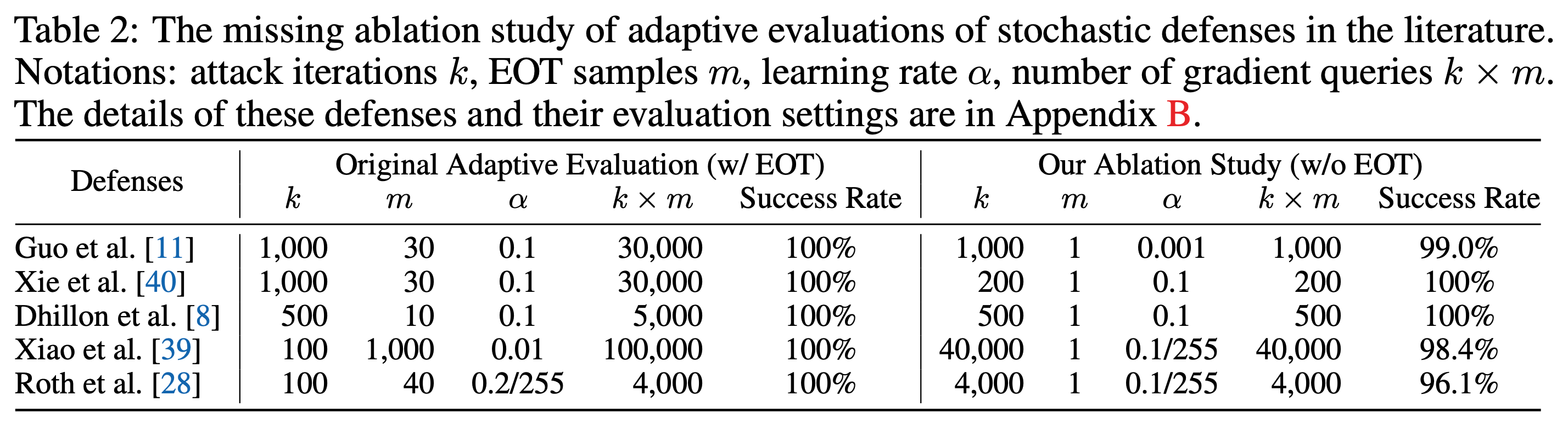
Athalye et al. [3] and Tramèr et al. [4] demonstrate adaptive evaluation of stochastic defenses with the application of expectation over transformations (EOT) [5]. The idea of EOT is fairly simple: because the transformations introduced by stochastic defenses create non-differentiable components in the model, the attacker should aim to evade many configurations of these components. This is done by ensembling the model in many of its configurations, corresponding each to a different random state, and then attacking this ensemble.
However, it remains unclear why EOT is required to break these stochastic defenses. While a commonly accepted explanation is that EOT computes the “correct gradients” of models with randomized components [3, 4], the necessity of such correct gradients has not been explicitly discussed. To fill this gap, we revisit stochastic defenses previously broken by EOT and examine their robustness without applying EOT.
Interestingly, we find that applying EOT is only beneficial when the defense is sufficiently randomized. Otherwise, standard attacks already perform well (as long as the standard attack runs for more iterations with a smaller learning rate). Put simply, the randomization’s contributions to robustness are overestimated. This observation implies that most stochastic defenses lack sufficient randomness to withstand even standard attacks designed for deterministic defenses.
Trade-offs between robustness and model invariance
When stochastic pre-processing defenses do have sufficient randomness, they must ensure that the utility of the defended model is preserved in the face of randomness. To achieve high utility, existing defenses mostly rely on applying the random pre-processing steps to the training data itself. This is designed to teach the model how to recognize inputs that have been transformed by the pre-processing defensive mechanism.
However, we find that this is precisely what makes stochastic pre-processing defenses fail. By teaching the model how to recognize pre-processed inputs well, we are essentially teaching the model to ignore pre-processing altogether. We will show why a bit more formally in the rest of this blog post.
A Simple Observation
If we consider a defense based on stochastic pre-processor \(t_\theta\), where the parameters \(\theta\) are draw from a randomization space \(\Theta\), the defended classifier \(F_\theta(x):=F(t_\theta(x))\) is invariant under the randomization space if
\[F(t_\theta(x)) = F(x), \forall \theta\in\Theta, x\in\mathcal{X}.\]As we can observe from the definition, invariance has direct implications on the performance of stochastic pre-processing defenses. If the classifier is invariant under the defense’s randomization space \(\Theta\) as is defined above, then the defense should not work – computing the model and its gradients over randomization \(\theta\in\Theta\) is the same as if \(t_\theta\) was not applied at all.
This observation can be formalized in the following binary classification task.
A Binary Classification Task
Having illustrated why invariance-based training explains why stochastic pre-processing defenses fail, we now provide a more concrete example with a binary classification task. We consider a class-balanced dataset consisting of input-label pairs \((x, y)\) with \(y\in\{-1,+1\}\) and \(x\rvert y\sim\mathcal{N}(y,1)\).
An \(\ell_\infty\)-bounded adversary perturbs the input with a small \(\epsilon\) to fool the classifier. We quantify the classifier’s robustness by its robust accuracy, that is, the ratio of correctly classified samples that remain correct after being perturbed by the adversary.

If we consider the application of a stochastic pre-processing defense, it is easy to develop the following four stages.
1. Undefended Classification.
The optimal linear classifier \(F(X):=\mathrm{sgn}(x)\) without any defense attains a certain level of robustness.
2. Defended Classification.
We introduce a defense \(t_\theta(x):=x+\theta\), where \(\theta\sim\mathcal{N}(1, \sigma^2)\) is the random variable parameterizing the defense. Here, the processed input follows a shifted distribution \(t_\theta(x)\sim\mathcal{N}(y+1,1+\sigma^2)\), attaining a higher level of robustness.
3. Defended Classification (Trained Invariance).
To preserve the defended model’s utility, the defense minimizes the risk over augmented data \(t_\theta(x)\), which leads to a new defended classifier \(F_\theta^+(x)=\mathrm{sgn}(x+\theta-1)\), reducing the previously attained robustness.
4. Defended Classification (Perfect Invariance).
Finally, the defense leverages the majority vote to obtain stable predictions, which finally produces a perfectly invariant defended classifier \(F_\theta^*(x)\to\mathrm{sgn}(x)=F(x)\), reducing to the original level of robustness.
The above procedure illustrates how stochastic pre-processing defenses first induce variance on the binary classifier we consider to provide adversarial robustness, and how they finally take back such variance to recover utility. This coupling can be extended to a general trade-off where we can explicitly control the invariance.

This trade-off demonstrates that stochastic pre-processing defenses provide robustness by explicitly reducing the model’s invariance to added randomized transformations.
Discussions
Finally, we discuss several questions that arose from our study of stochastic pre-processing defenses. We invite you to read our paper for more details.
What do pre-processing defenses really do? Existing stochastic pre-processing defenses do not introduce inherent robustness to the prediction task. Instead, they shift the input distribution through randomness and transformations, which results in variance and introduces errors during prediction. The observed “robustness”, in an unusual meaning for this literature, is a result of these errors. This is fundamentally different from the inherent robustness provided by adversarial training [6]. Although defenses like adversarial training still cost accuracy, they do not intentionally introduce errors like stochastic pre-processing defenses.
Should we abandon randomized defenses? We should not abandon randomized defenses but utilize randomness in new ways. One promising approach is dividing the problem into orthogonal subproblems. For example, some speech problems (such as keyword spotting) are inherently divisible in the spectrum space, and vision tasks are divisible by introducing different modalities [7], independency [8], or orthogonality [9]. In such cases, randomization forces the attack to target all possible (independent) subproblems, where the model performs well on each (independent and) non-transferable subproblem. As a result, defenses can decouple robustness and invariance, hence avoiding the pitfall of previous randomized defenses.
What are the concrete settings in which randomized defenses work? Randomized defenses do make the attack harder in the black-box setting. In such a case, the defense practically introduces noise to the attack’s optimization procedure, making it difficult for a low-query adversary to find adversarial examples that consistently cross the probabilistic decision boundary. However, we cannot find evidence that stochastic pre-processing defenses work in the white-box setting. Other forms of randomness discussed above are more promising. The only exception is randomized smoothing, which remains an effective tool to certify the inherent robustness of a given decision.
References
[1] Edward Raff, Jared Sylvester, Steven Forsyth, and Mark McLean. Barrage of Random Transforms for Adversarially Robust Defense. CVPR 2019.
[2] Chawin Sitawarin, Zachary Golan-Strieb, and David Wagner. Demystifying the Adversarial Robustness of Random Transformation Defenses. ICML 2022.
[3] Anish Athalye, Nicholas Carlini, David Wagner. Obfuscated Gradients Give a False Sense of Security: Circumventing Defenses to Adversarial Examples. ICML 2018.
[4] Florian Tramer, Nicholas Carlini, Wieland Brendel, Aleksander Madry. On Adaptive Attacks to Adversarial Example Defenses. NeurIPS 2020.
[5] Anish Athalye, Logan Engstrom, Andrew Ilyas, Kevin Kwok. Synthesizing Robust Adversarial Examples. ICML 2018.
[6] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, Adrian Vladu. Towards Deep Learning Models Resistant to Adversarial Attacks. ICLR 2018.
[7] Karren Yang, Wan-Yi Lin, Manash Barman, Filipe Condessa, Zico Kolter. Defending Multimodal Fusion Models Against Single-Source Adversaries. CVPR 2021.
[8] Wan-Yi Lin, Fatemeh Sheikholeslami, jinghao shi, Leslie Rice, J Zico Kolter. Certified Robustness Against Physically-Realizable Patch Attack via Randomized Cropping. ICML 2021 Workshop.
[9] Zhuolin Yang, Linyi Li, Xiaojun Xu, Shiliang Zuo, Qian Chen, Pan Zhou, Benjamin Rubinstein, Ce Zhang, Bo Li. TRS: Transferability Reduced Ensemble via Promoting Gradient Diversity and Model Smoothness. NeurIPS 2021.